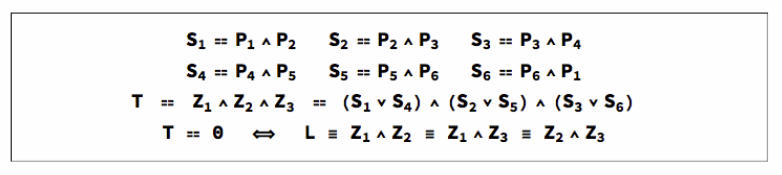Grassmann algebra is an algebra for Geometry
[BACK to Geometry Page: 1]
Continuation Page: 2.
On this page we continue a series of graphics from Volume 1 using
the entities and operations of the algebra as direct inputs to the
drawing routines. Operations include the exterior product for
combining entities, and the regressive product for finding their
common components. The entities of the algebra can represent
vectors, bivectors and multivectors, points, lines, planes, and
multiplanes. Projective geometry of n-space is subsumed by the
algebra, and many of its theorems reduced to the vanishing of
products of the entities.
From these entities, higher order objects can be defined: for example
curves, surfaces, simplexes or regions of space. Expressions involving
these may often be considered as a prescription to construct them.
Grassmann algebra is an algebra par excellence for geometry.
Animated with systems like Mathematica it also has the potential to
become an algebra for dynamic simulations in fields such as physics,
engineering and game development.
© John Browne 2018.
[ Home ] [ Biography ] [ Bibliography ] [ Book Contents ] [ Chapter 1 PDF ] [ Geometry ] [ Book ] [ Contact ]

Pascal lines
Below is a plot of the 60 bound vectors and bivectors used to represent the 60 Pascal lines and lines at infinity of the 60 different hexagons formed from the 6 vertices of a regular hexagon. The lack of apparent symmetry is an artifact caused by the extra information the bound vectors and bivectors portray.
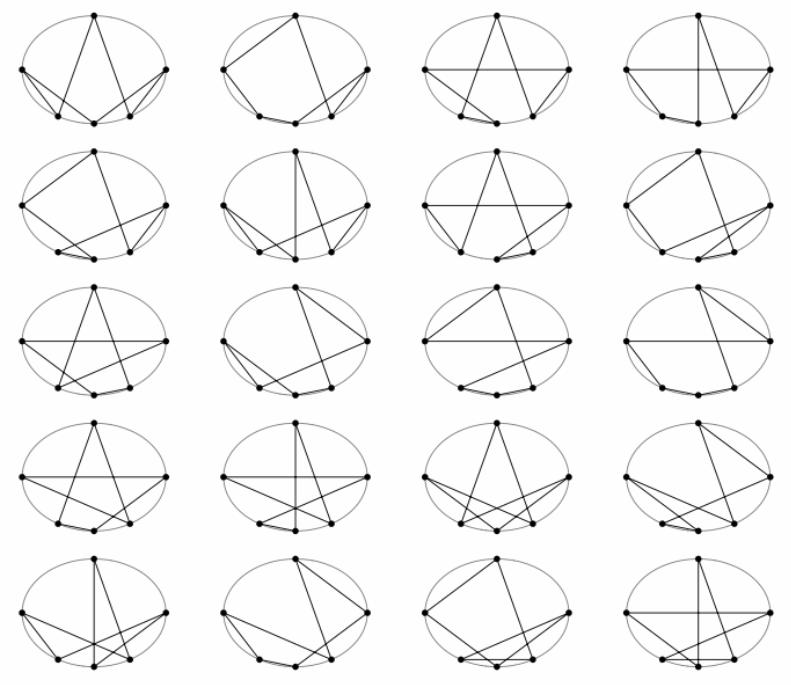
Hexagons in an ellipse
Given six points on a conic, there are 60 different hexagons which can be constructed: an initial point may be joined to a second point in five ways, the second point to a third point in 4 ways and so on, leading to 5! ways of constructing a hexagon. However for each one there corresponds the same hexagon traversed in the reverse order, thus leading to just 60 different hexagons. Pascal's Theorem establishes a line associated with any hexagon inscribed in a conic, so to each of these 60 hexagons will correspond a Pascal line. Here are 20 of the hexagons.

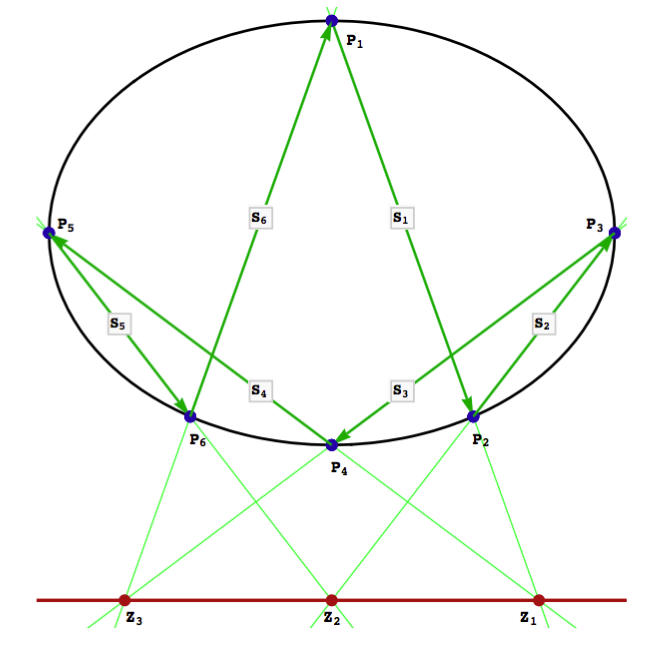
Pascal's Theorem
Pascal's Theorem and its converse state that If a hexagon in inscribed in a conic, then opposite sides intersect in collinear points. If opposite sides of a hexagon intersect in three collinear points, then the hexagon may be inscribed in a conic. The graphic below shows 6 vertices P defining the sides S of a hexagon whose opposite sides intersect in points Z, the exterior product of which is T. If T is zero, the points Z lie on a line L called the Pascal line of the hexagon. Pascal's Theorem says that if the points P lie on a conic then T is zero. The converse says that if T is zero, the points P lie on a conic. T and L are constructed from the points P according to the formulae below.